The geoid is an equipotential surface of the Earth’s gravity field that is closely associated with the mean ocean surface. "Closely associated" can be defined in a number of ways [Rapp, 1995]. A working concept is that the mean difference between a geoid and the mean ocean surface should be zero. Deviations between the mean ocean surface and the geoid represent (primarily) mean Dynamic Ocean Topography (DOT). The standard deviation of the DOT is approximately ± 62 cm, with extreme values from about 80 cm to about –213 cm, the latter in the Antarctic Circumpolar Regions (e.g., 66^°S, 356^°E). Plots of the DOT can be seen in numerous papers and reports as well as in sections 7 and 10 of this report.

The geoid undulation is the separation between the geoid and an ellipsoid whose surface is equipotential. The ellipsoid is defined by four quantities: a (equatorial radius), f (inverse flattening), w (angular velocity), and GM (geocentric gravitational constant). Alternate quantities are possible. For example, the second-degree zonal harmonic, J₂, is a primary quantity in the definition of The Geodetic Reference System, 1980 [Moritz, 1992].

The definition of the geoid is complicated by the permanent deformation of the Earth caused by the presence of the Sun and the Moon. Consideration of these permanent tidal effects has led to the definition of three types of geoids and three types of reference ellipsoids [Ekman, 1989, 1995; Rapp et al., 1991; Bursa, 1995a]. The three geoids are described as follows:

1. Tide-free (or nontidal)—This geoid would exist for a tide-free Earth with all (direct and indirect) effects of the Sun and Moon removed.
1. Mean—This geoid would exist in the presence of the Sun and the Moon (or, equivalently, if no permanent tidal effects are removed).
1. Zero—This geoid would exist if the permanent direct effects of the Sun and Moon are removed, but the indirect effect component related to the elastic deformation of the Earth is retained.

Conceptually, one would have analogous definitions of an ellipsoid that would be associated with the corresponding type of geoid. We could have a tide-free ellipsoid, a mean-tide ellipsoid, or a zero-tide ellipsoid. There will be a different equatorial radius and flattening associated with each type of ellipsoid.

If one considers a reference ellipsoid fixed by a definition of a and f, one will have different geoid undulations depending on the type of geoid undulation (tide free, mean, zero) that is being studied. Equations to convert from one system to another may be found in Ekman [1989], Rapp [1994], etc.. Let N_m be the mean geoid undulation, N_n the nontidal one, and N_z be the zero geoid undulation. Then we have [Ekman, 1989]:

N_m–N_z = 9.9–29.6 sin^2f cm (11.1–1)

N_z–N_n = k (9.9–29.6 sin^2f ) cm (11.1–2)

N_m–N_n = (1+k) (9.9–29.6 sin^2f ) cm (11.1–3)

where k is a Love number usually taken as 0.3.

The issue in the determination of the undulations for the EGM96 model is, then, in what tide system are such undulations to be given. In the case that the geoid undulations are to be used with satellite altimeter data for the determination (e.g.) of dynamic ocean topography (see eq. 5.5.1–3), the undulations must be given in a system consistent with that used for the determination of the sea surface height. This is normally the mean tide system, so that geoid undulation (N_m) in the mean tide system is used. For other applications, the situation is not as clear.

At the 1983 IAG General Assembly in Hamburg, a resolution (16) was passed that states, in part "...the indirect effect due to the permanent yielding of the Earth be not removed." This recommendation suggests that the appropriate geoid to consider is the zero geoid with the corresponding zero geoid undulation of interest.

Also pertinent to the discussions are the conventions used in the reporting of station positions on the surface of the Earth determined from satellite (e.g., GPS) positioning procedures considering permanent tide issues. Recommendations can be found in the procedures conceptually adopted as part of the International Earth Rotation Service (IERS). These procedures are described in the IERS Conventions [1996] [McCarthy, 1996]. The effect of permanent deformation is described in Section 7, p. 65. In this case, the total permanent deformation is removed in the initial tidal correction, followed by the restitution of the indirect effect: "The restitution of the indirect effect of the permanent tide is done to be consistent with the XVIII IAG General Assembly Resolution 16; ..."

An important application of the geoid undulation will be the determination of the orthometric height (H) of a point from the ellipsoidal height (h). From eq. (5.2.1–1) we have:

H = h–N (11.1–4)

The H value will be given with respect to the geoid whose undulations, with respect to a specific ellipsoid, are given by N. It is now clear that h and N must be given in a consistent tide system. Although IAG Resolution 16 recommends a zero-tide system, an informal survey of several groups involved with position determination indicated that position (and clearly heights) were being reported in a tide-free system. Although the difference between heights in a tide-free and zero-tide system are on the order of 10 cm, it is important for consistency purposes that h and N be given in the same system. Consequently, a decision was reached by the joint project that the preferred tide system would be the tide-free system and that the geoid undulations will be for the tide-free geoid.

We now determine the value of z _z defined by eq. (5.2.1–8). As written, the value of z _z will be dependent on latitude through the variation of r and g . However, this variation is sufficiently small that mean values can be taken. One then rewrites (5.2.1–8) as follows:

(11.2–1)

where r and g are regarded as mean values over the ellipsoid. Based on the WGS84 ellipsoid, we have [Defense Mapping Agency, 1991, Tables 3.1 and 3.2]:

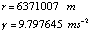(11.2–2)

We next need to consider the determination of GM, GM₀, W₀, U₀. The value of GM₀ will be that adopted for the updated GM of the WGS84 ellipsoid. This value is 3.986004418x10¹⁴ m³s^–2, which is identical to that given in the IERS Numerical Standards [McCarthy, 1996, Table 4.1]. The best estimate of GM can be taken as the same value based on the recommendations of the IAG Special Commission SC3, Fundamental Constants [Bursa, 1995b, p. 381]. With this situation, the first term in eq. (11.2–1) is zero.

In order to calculate the second term on the right side of (11.2–1), one first needs to adopt or determine the ideal potential on the surface of the geoid followed by the determination of U₀ based on the parameters of the enhanced WGS84 ellipsoid. We start with the adoption of the following estimate of W₀ from Bursa [1995b, eq. (39)]:

W₀ = 62 636 856.88 m²s^–2 (11.2–3)

This value is consistent with a set of a and f values given in a consistent tide system. In the tide-free system in which we have chosen to work, we have [Bursa et al., 1995b, eq. (24) and (27)]:

a = 6378136.46 m (11.2–4)

f = 1/298.25765 (11.2–5)

For determination of U₀ the parameters of the enhanced WGS84 ellipsoid are:

a = 6378137.00 m (11.2–6)

f = 1/298.257223563 (11.2–7)

GM = 3.986004418 x 10¹⁴ m³ s^–2 (11.2–8)

w = 7292115 x 10^–11 sec ^–2 (11.2–9)

The value of w is the mean angular velocity of the Earth. Using these four values, the corresponding U₀ value on the surface of the ellipsoid can be calculated [Heiskanen and Moritz, 1967, eq. (2–61)]; one finds:

U₀ = 62 636 851.71 m³s^–2 (11.2–10)

Using the values of W₀ and U₀ in eq. (11.2–1) yields:

z _z = –52.8 cm, (11.2–11)

which will be rounded to –53 cm for actual computation.

An alternative procedure is to calculate the zero-degree term based on the first of eq. (2–200) in Heiskanen and Moritz [1967, p.111]. One has:

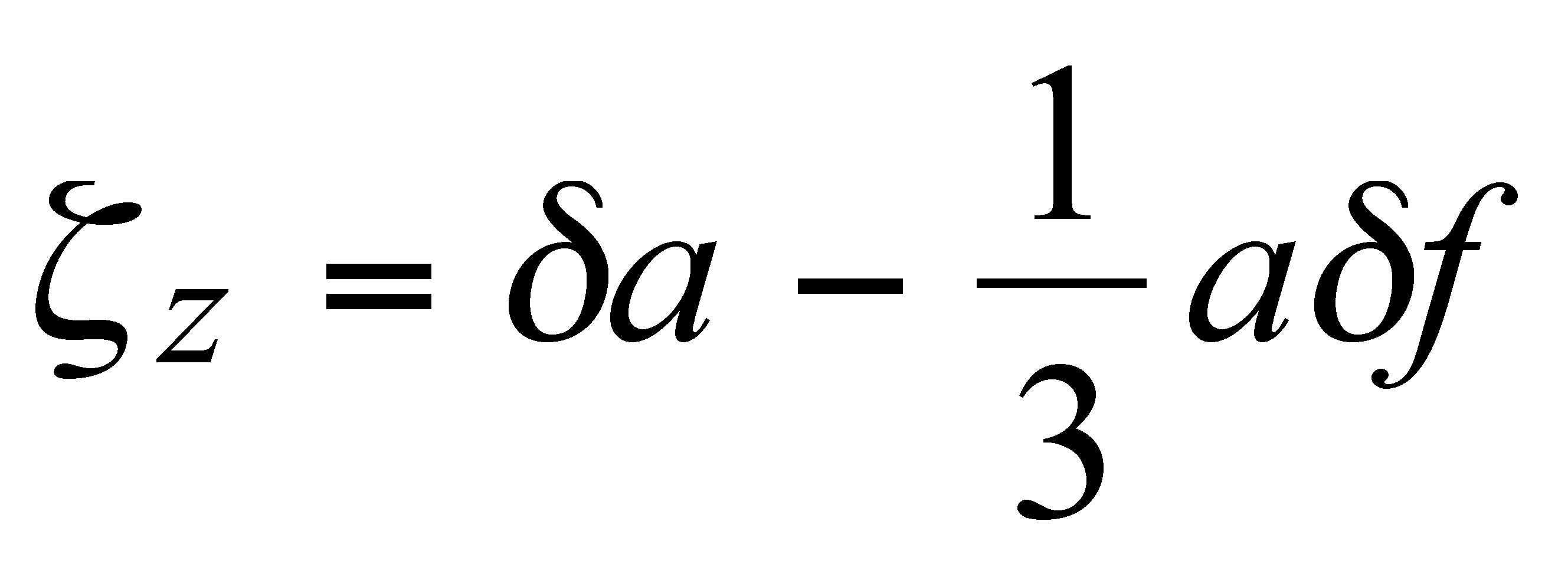(11.2–12)

where d a and d f are the differences, ideal minus reference value, for the equatorial radius and flattening. Using the a values from (11.2–4) and (11.2–6) and the flattening values from (11.2–5) and (11.2–7), one finds from (11.2–12) a value of z _z equal to –52.9 cm, which agrees, within the accuracy of the spherical approximation of (11.2–12) with the value given by (11.2–11).

In summary, we adopt the following value of z _z:

z _z = –53 cm (11.2–13)

The use of this value in the undulation computation enables the undulation to refer to the WGS84 ellipsoid defined by the parameters in eqs. (11.2–6 to –9). One must recognize that this calculation is subject to numerous error sources, primarily in the determination of the ideal equatorial radius. It would not be unreasonable to attach a standard deviation of ± 10 cm to the z _z value given in (11.2–13).

The geoid undulation calculated from eq. (5.2.1–12) refers to a coordinate system the origin of which is at the center of mass of the Earth. This is because the summation shown starts from degree two, implicitly forcing the degree one terms to be zero.

In practice, the location of the center of mass, as well as the alignment of the axes of the reference frame, is defined by the system in which the geopotential model, station coordinates, etc., are estimated. The system used for the model development is described in Section 7.3.5, where it is shown that the effective reference frame in which EGM96 was estimated was practically equivalent to the reference frame, WGS84 (G873), implemented as the current (November 1996) operational WGS84 reference frame [Malys, 1996]. This frame is considered to be coincident with the ITRF94 to better than 2 cm.

In summary, the geoid undulations, as computed with the procedures described in this section, will refer to the WGS84 ellipsoid, whose origin is at the center of mass of Earth, as defined by WGS84 (G873)/ITRF94, and whose axes are aligned with the indicated reference frames.

The calculation of the geoid undulation takes place using eq. (5.2.1–23/26):

(11.4–1)

where z _z = –0.53 m, C(q , l ) is the sum of three corrections terms and z *(r_E,q , l ) is:

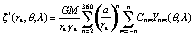(11.4–2)

where the subscript E indicates an evaluation for a point on the ellipsoid at a geocentric latitude corresponding to 90^o – q ^o. The even-degree zonal value of C_nm represents the difference between the EGM96 coefficient and the reference values computed for the WGS84 ellipsoid with the constants defined by eq. (11.2–6 to –9). The values calculated are those of the even zonal coefficients (J_2n) in a representation of the potential as defined by the equation below (2–91) in Heiskanen and Moritz [1967, p. 73]. These coefficients are related to the C_2n,₀ coefficients of (11.4–2), as follows:

(11.4–3)

The value of J_2n were computed using eq. (2–92) of Heiskanen and Moritz [1967, p.73] using subroutine GRS written by N. Pavlis [private communication]. One has:

J₂ = 0.1082 6298 2131 x 10^–2

J₄ = –0.2370 9112 0053 x 10^–5

J₆ = 0.6083 4649 8882 x 10^–8 (11.4–4)

J₈ = –0.1426 8108 7920 x 10^–10

J₁₀ = 0.1214 3927 5882 x 10^–13

The value of N can be computed in two ways. The first procedure is to calculate a grid of z * and C values using efficient software for rapid calculation of gridded values using high-degree spherical harmonic expansions. Adding the z *, C, and z _z values yields the gridded values. The grid interval selected by NIMA for this calculation was 0.25°x0.25° (15´x15´). Values can be interpolated to an arbitrary point using a spline interpolation procedure to assure 1- to 2-cm interpolation precision. The grid of values for the EGM96 geoid undulation with respect to the WGS84 can be found at the following NIMA Web site:

http://164.214.2.59/geospatial/products/GandG/wgs-84/geos.html

An alternative procedure to the gridding process is the calculation of the N value at a specified location. This procedure requires the evaluation of two spherical harmonic expansions (one for z * and one for C) followed by the addition of z _z according to eq. (11.4–1). This procedure has been implemented by a modification of the program described by Rapp [1982]. The two major changes were: 1) the deletion of all computations except those related to the z (equivalent to the geoid undulation computation in the reference) and 2) the incorporation of the calculation of C(q ,l ) given the spherical harmonic representation of the correction term. The modified program is called F477NONLY and has also been placed on the Web site noted above. Also included are the EGM96 coefficients and the coefficients of the correction term C based on the EGM96 coefficients.

Whether one uses the gridded values to interpolate the undulation or the point calculation using the software provided, the result should be the same within 1 or 2 cm. The value will be the geoid undulation, in the tide-free system with respect to the WGS84 ellipsoid, implied by the EGM96 geopotential model.

• Back to Abstract of NASA TP-1998-206861.
• Back to Table of Contents.
• Back to the EGM96 web page.